| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 11066 | Accepted: 1673 |
Description
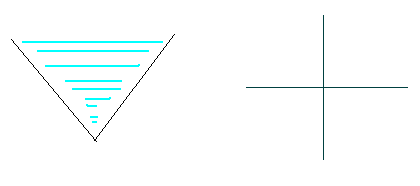
Input
Output
Sample Input
2 0 1 1 0 1 0 2 1 0 1 2 1 1 0 1 2
Sample Output
1.00 0.00
感动到cry。。。终于A掉了。
我的做法是这样的:
有三个重要的点,一个是两条线段的交点,设为crossp
第二个是末端点中较低的点(所以读入的时候adjust一下,线段方向维护成由低指向高),设为lowp
第三个是由lowp做平行线,交到另一条直线(anotherline)得到点p3
雨是垂直下落。
一般的情况只要求这三个点组成的三角形的面积就行了(叉积或者h*c/2都可以) 两种写法都可以A
主要是一些误解情况的判断。
首先,不相交的话,肯定无解。
所以先判断下相交。
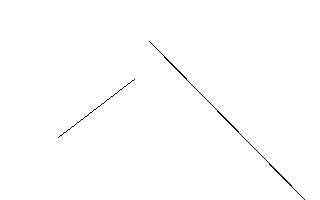
细分的话,如果有一条直线平行x轴,那么肯定无解。
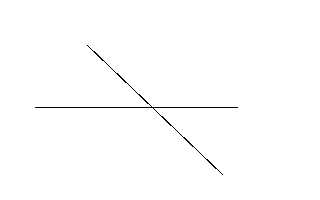
接下来是,crossp正好和lowp重合,肯定无解。
然而如果用c*h/2的话,2,3两种情况可以不用单独考虑,因为会得出h==0,答案自然为0
接下来比较难想到的是,口被封住的情况。

虽然我想到了这种情况,但是判定条件想错了。
我误以为两个末端点在p3的同侧的话,口就会无解。
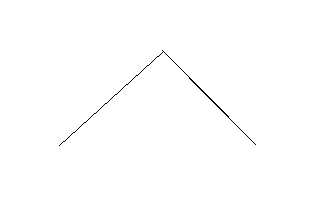
但如下图

这种情况却是有解的,答案不为0
这步判定想错是我WA了多次最主要的原因QAQ
不过只要稍微改动下就好
只有x在lowp那条线的左边且lowp在anotherline末端点的左边
或者x在lowp那条线的右边且lowp在anotherline末端点的右边 口才会被封住。
1 int sameside(point p1,point p2) 2 { 3 // p1.output(); 4 // p2.output(); 5 if (dblcmp(x-p2.x)<=0&&dblcmp(p2.x-p1.x)<=0) return 1; 6 if (dblcmp(x-p2.x)>=0&&dblcmp(p2.x-p1.x)>=0) return 1; 7 return 0; 8 }
因为一个细节又WA了一次。
上面的代码一开始忘写了等号。
如果但实际上末端点的横坐标相等,也是无解的。

1 /************************************************************************* 2 > File Name: code/poj/2826.cpp 3 > Author: 111qqz 4 > Email: rkz2013@126.com 5 > Created Time: 2015年11月06日 星期五 16时07分21秒 6 ************************************************************************/ 7 8 #include<iostream> 9 #include<iomanip> 10 #include<cstdio> 11 #include<algorithm> 12 #include<cmath> 13 #include<cstring> 14 #include<string> 15 #include<map> 16 #include<set> 17 #include<queue> 18 #include<vector> 19 #include<stack> 20 #include<cctype> 21 #define fst first 22 #define sec second 23 #define lson l,m,rt<<1 24 #define rson m+1,r,rt<<1|1 25 #define ms(a,x) memset(a,x,sizeof(a)) 26 using namespace std; 27 const double eps = 1E-10; 28 const int dx4[4]={1,0,0,-1}; 29 const int dy4[4]={0,-1,1,0}; 30 typedef long long LL; 31 const int inf = 0x3f3f3f3f; 32 const double pi = acos(-1.0); 33 int dblcmp(double d) 34 { 35 return d < -eps ? -1 : d > eps; 36 } 37 inline double sqr(double x){return x*x;} 38 struct point 39 { 40 double x,y; 41 point(){} 42 point(double _x,double _y): 43 x(_x),y(_y){}; 44 void input() 45 { 46 scanf("%lf%lf",&x,&y); 47 } 48 void output() 49 { 50 printf("%.2f %.2f\n",x,y); 51 } 52 bool operator==(point a)const 53 { 54 return dblcmp(a.x-x)==0&&dblcmp(a.y-y)==0; 55 } 56 bool operator<(point a)const 57 { 58 return dblcmp(a.x-x)==0?dblcmp(y-a.y)<0:x<a.x; 59 } 60 double len() 61 { 62 return hypot(x,y); 63 } 64 double len2() 65 { 66 return x*x+y*y; 67 } 68 double distance(point p) 69 { 70 return hypot(x-p.x,y-p.y); 71 } 72 double distance2(point p) 73 { 74 return sqr(x-p.x)+sqr(y-p.y); 75 } 76 point add(point p) 77 { 78 return point(x+p.x,y+p.y); 79 } 80 point operator + (const point & p) const{ 81 return point(x+p.x,y+p.y); 82 } 83 point sub(point p) 84 { 85 return point(x-p.x,y-p.y); 86 } 87 point operator - (const point & p) const{ 88 return point(x-p.x,y-p.y); 89 } 90 point mul(double b) 91 { 92 return point(x*b,y*b); 93 } 94 point div(double b) 95 { 96 return point(x/b,y/b); 97 } 98 double dot(point p) 99 { 100 return x*p.x+y*p.y; 101 } 102 double operator * (const point & p) const{ 103 return x*p.x+y*p.y; 104 } 105 double det(point p) 106 { 107 return x*p.y-y*p.x; 108 } 109 double operator ^ (const point & p) const{ 110 return x*p.y-y*p.x; 111 } 112 double rad(point a,point b) 113 { 114 point p=*this; 115 return fabs(atan2(fabs(a.sub(p).det(b.sub(p))),a.sub(p).dot(b.sub(p)))); 116 } 117 point trunc(double r) 118 { 119 double l=len(); 120 if (!dblcmp(l))return *this; 121 r/=l; 122 return point(x*r,y*r); 123 } 124 point rotleft() 125 { 126 return point(-y,x); 127 } 128 point rotright() 129 { 130 return point(y,-x); 131 } 132 point rotate(point p,double angle)//绕点p逆时针旋转angle角度 133 { 134 point v=this->sub(p); 135 double c=cos(angle),s=sin(angle); 136 return point(p.x+v.x*c-v.y*s,p.y+v.x*s+v.y*c); 137 } 138 139 int sameside(point p1,point p2) 140 { 141 // p1.output(); 142 // p2.output(); 143 if (dblcmp(x-p2.x)<=0&&dblcmp(p2.x-p1.x)<=0) return 1; 144 if (dblcmp(x-p2.x)>=0&&dblcmp(p2.x-p1.x)>=0) return 1; 145 return 0; 146 } 147 double gettrianglearea(point b,point c) 148 { 149 return ((b.x-x)*(c.y-y)-(b.y-y)*(c.x-x))/2; 150 } 151 }; 152 struct line 153 { 154 point a,b; 155 line(){} 156 line(point _a,point _b) 157 { 158 a=_a; 159 b=_b; 160 } 161 bool operator==(line v) 162 { 163 return (a==v.a)&&(b==v.b); 164 } 165 //倾斜角angle 166 line(point p,double angle) 167 { 168 a=p; 169 if (dblcmp(angle-pi/2)==0) 170 { 171 b=a.add(point(0,1)); 172 } 173 else 174 { 175 b=a.add(point(1,tan(angle))); 176 } 177 } 178 //ax+by+c=0 179 line(double _a,double _b,double _c) 180 { 181 if (dblcmp(_a)==0) 182 { 183 a=point(0,-_c/_b); 184 b=point(1,-_c/_b); 185 } 186 else if (dblcmp(_b)==0) 187 { 188 a=point(-_c/_a,0); 189 b=point(-_c/_a,1); 190 } 191 else 192 { 193 a=point(0,-_c/_b); 194 b=point(1,(-_c-_a)/_b); 195 } 196 } 197 void input() 198 { 199 a.input(); 200 b.input(); 201 } 202 void adjust() //调整为由低指向高 203 { 204 if (dblcmp(a.y-b.y)>0) swap(a,b); 205 } 206 double length() 207 { 208 return a.distance(b); 209 } 210 double getk() 211 { 212 // printf("*********\na.x: %f a.y %f b.x : %f b.y : %f\n ****************\n",a.x,a.y,b.x,b.y); 213 return (b.y-a.y)/(b.x-a.x); 214 } 215 double angle()//直线倾斜角 0<=angle<180 216 { 217 double k=atan2(b.y-a.y,b.x-a.x); 218 if (dblcmp(k)<0)k+=pi; 219 if (dblcmp(k-pi)==0)k-=pi; 220 // cout<<"ang1:"<<k<<endl; 221 // cout<<"k:"<<tan(k)<<endl; 222 return k; 223 } 224 //点和线段关系 225 //1 在逆时针 226 //2 在顺时针 227 //3 平行 228 int relation(point p) 229 { 230 int c=dblcmp(p.sub(a).det(b.sub(a))); 231 if (c<0)return 1; 232 if (c>0)return 2; 233 return 3; 234 } 235 bool pointonseg(point p) 236 { 237 return dblcmp(p.sub(a).det(b.sub(a)))==0&&dblcmp(p.sub(a).dot(p.sub(b)))<=0; 238 } 239 bool parallel(line v) 240 { 241 return dblcmp(b.sub(a).det(v.b.sub(v.a)))==0; 242 } 243 //2 规范相交 244 //1 非规范相交 () 245 //0 不相交 246 int segcrossseg(line v) 247 { 248 int d1=dblcmp(b.sub(a).det(v.a.sub(a))); 249 int d2=dblcmp(b.sub(a).det(v.b.sub(a))); 250 int d3=dblcmp(v.b.sub(v.a).det(a.sub(v.a))); 251 int d4=dblcmp(v.b.sub(v.a).det(b.sub(v.a))); 252 if ((d1^d2)==-2&&(d3^d4)==-2)return 2; 253 return (d1==0&&dblcmp(v.a.sub(a).dot(v.a.sub(b)))<=0|| 254 d2==0&&dblcmp(v.b.sub(a).dot(v.b.sub(b)))<=0|| 255 d3==0&&dblcmp(a.sub(v.a).dot(a.sub(v.b)))<=0|| 256 d4==0&&dblcmp(b.sub(v.a).dot(b.sub(v.b)))<=0); 257 } 258 int linecrossseg(line v)//*this seg v line 259 { 260 int d1=dblcmp(b.sub(a).det(v.a.sub(a))); 261 int d2=dblcmp(b.sub(a).det(v.b.sub(a))); 262 if ((d1^d2)==-2)return 2; 263 return (d1==0||d2==0); 264 } 265 point crosspoint(line v) 266 { 267 double a1=v.b.sub(v.a).det(a.sub(v.a)); 268 double a2=v.b.sub(v.a).det(b.sub(v.a)); 269 return point((a.x*a2-b.x*a1)/(a2-a1),(a.y*a2-b.y*a1)/(a2-a1)); 270 } 271 }li[10]; 272 int main() 273 { 274 #ifndef ONLINE_JUDGE 275 freopen("in.txt","r",stdin); 276 #endif 277 278 int T; 279 scanf("%d",&T); 280 while (T--) 281 { 282 li[1].input();li[1].adjust(); 283 li[2].input();li[2].adjust(); 284 if (li[1].segcrossseg(li[2])==0) //不相交 285 { 286 puts("0.00"); 287 continue; 288 } 289 290 point crossp=li[1].crosspoint(li[2]); 291 point lowp; 292 int anotherline; 293 if (li[1].b.y<li[2].b.y) 294 { 295 lowp=li[1].b; 296 anotherline=2; 297 } 298 else 299 { 300 lowp=li[2].b; 301 anotherline=1 ; 302 } 303 304 point p3; 305 if (dblcmp(li[anotherline].a.x-li[anotherline].b.x)==0) 306 { 307 p3.x=li[anotherline].a.x; 308 p3.y=lowp.y; 309 } 310 else 311 { 312 double dy =lowp.y-li[anotherline].a.y; 313 double k = li[anotherline].getk(); 314 p3.x=li[anotherline].a.x+dy*1.0/k; 315 p3.y=lowp.y; 316 } 317 double h = lowp.y-crossp.y; 318 if (dblcmp(h)==0) 319 { 320 puts("0.00"); 321 continue; 322 } 323 if (p3.sameside(li[anotherline].b,li[anotherline%2+1].b)==1) 324 { 325 puts("0.00"); 326 continue; 327 } 328 double c = fabs(lowp.x-p3.x); 329 330 double ans = h*c/2; 331 // double ans = lowp.gettrianglearea(crossp,p3); 332 printf("%.2f\n",fabs(ans)); 333 334 335 } 336 337 338 #ifndef ONLINE_JUDGE 339 #endif 340 fclose(stdin); 341 return 0; 342 }
poj 2826 An Easy Problem?! (线段相交问题终极版...并不easy)
原文:http://www.cnblogs.com/111qqz/p/4945787.html