Given a matrix of m x n elements (m rows, n columns), return all elements of the matrix in spiral order.
For example,
Given the following matrix:
[ [ 1, 2, 3 ], [ 4, 5, 6 ], [ 7, 8, 9 ] ]
You should return [1,2,3,6,9,8,7,4,5].
这道题只有笨方法,就是老老实实地遍历输入的二维数组,得到结果。
但是在遍历时有个技巧,就是按照环来遍历。(x, y)为遍历点的坐标。我们发现,当遍历完一圈后,(x, y)又会回到起点。所以对于接下来里面一圈的遍历,只需x++, y++即可。
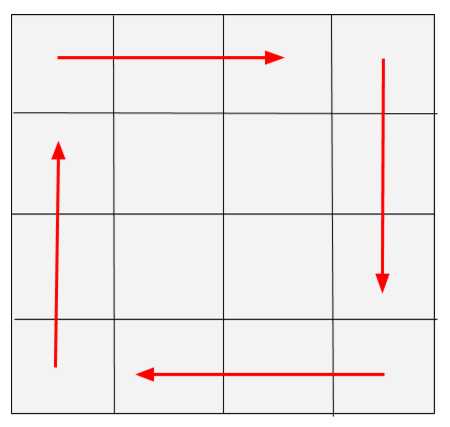
由于输入不一定是正方形,有可能最后剩的一圈是一行或一列,此时根据省下的行数/列数判断,另行处理。
1 public class Solution { 2 public List<Integer> spiralOrder(int[][] matrix) { 3 List<Integer> result = new ArrayList<Integer>(); 4 if (matrix == null || matrix.length < 1) 5 return result; 6 int m = matrix.length, n = matrix[0].length, x = 0, y = 0; 7 while (m > 0 && n > 0) { 8 // If only one row left 9 if (m == 1) { 10 for (int i = 0; i < n; i++) 11 result.add(matrix[x][y++]); 12 break; 13 } 14 // If only one column left 15 if (n == 1) { 16 for (int i = 0; i < m; i++) 17 result.add(matrix[x++][y]); 18 break; 19 } 20 // Otherwise, we traverse in a circle 21 // Left to Right 22 for (int i = 0; i < n - 1; i++) 23 result.add(matrix[x][y++]); 24 // Up to Down 25 for (int i = 0; i < m - 1; i++) 26 result.add(matrix[x++][y]); 27 // Right to Left 28 for (int i = 0; i < n - 1; i++) 29 result.add(matrix[x][y--]); 30 // Down to Up 31 for (int i = 0; i < m - 1; i++) 32 result.add(matrix[x--][y]); 33 x++; 34 y++; 35 m -= 2; 36 n -= 2; 37 } 38 return result; 39 } 40 }
原文:http://www.cnblogs.com/ireneyanglan/p/4890842.html