[数据挖掘课程笔记]Naïve Bayesian Classifier

朴素贝叶斯模型

      1) X:一条未被标记的数据

      2) H:一个假设，如H=X属于C_i类

      根据贝叶斯公式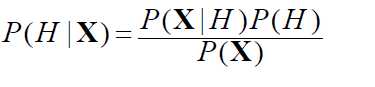

       把X表示为（x₁,x₂,....x_n） x₁,x₂,....x_n表示X在各个特征上的值。

       假设有c_1,c_2,c_3...c_m个类别。

       那么这个对X的分类问题就可以转化为找出使P（c_i|X）最大的类别c_i作为分类结果

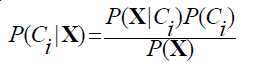
        由于我们只需要找出P（c_i|X）的相对最大值，那么即找出P（X|c_i）P（c_i）的最大值即可

      N为整个训练集的个数

      P（c_i）=count(c_i)/N

      假设X的各个属性是相互独立的：

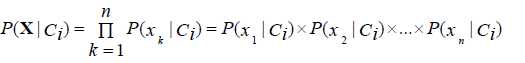
       那么，如何求P（x_i|c_j）呢？

     若第i个属性是离散型的，那么 P（x_i|c_j） =  所有分类为c_j并且第i个属性值等于x_i的数据个数/所有分类为c_j的数据个数

     若第i个属性是连续型的，假设这个连续型属性服从高斯分布：

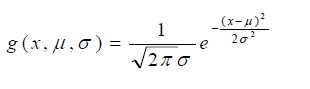
     那么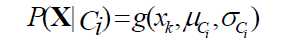

    其中μ_ci为所有数据类型为c_i并且第i个属性值为x_i的平均值

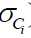          为所有数据类型为c_i并且第i个属性值为x_i的方差

[数据挖掘课程笔记]Naïve Bayesian Classifier

原文：http://www.cnblogs.com/leeshum/p/4873346.html