又是一个令人头疼的题目啊。。。。
这次又增加难度了!!!找二维数组中的最大子数组,要求联通即可:
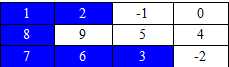
开始自己想法是枚举,然后找规律,后来发现这种方法实在是弱爆了,而且不好实现,后来通过查阅资料,发现大牛们都推荐动态规划,下面把思想陈述一下:
首先,将二维问题降维处理:
例如,用2 维数组a[1 : m][1 : n]表示给定的m行n列的整数矩阵。子数组a[i1 : i2][j1 : j2]表示左上角和右下角行列坐标分别为(i1, j1)和(i2, j2)的子矩阵。
先按照行排列出所有可能区间,然后,再去求列的范围。
更详细的,当行区间确定之后,剩下就是确定列区间了,一旦确定列区间,最大子矩阵就确定了。
当行区间确定之后,求列区间的方法,可以转化成一维数组的最大连续子序列的问题:对行区间[i1, j1],依次对列进行求和,就得到n个数据的以为数组,根据最大连续子序列的和的求法,就可以获得连续子序列最大和。
仍然用nGreatestNum来记录最大值,算出一个子矩阵的和,就进行比较即可。
算法在设计中。。。
二维数组之后续篇章(张硕---李帅),布布扣,bubuko.com
原文:http://www.cnblogs.com/zsjy/p/3634613.html