6 10 + 1 1 1 2 1 1 3 2 2 4 5 + - 1 4 3 2 3 5 5 4 6 2 5 - 1 6 5 3 4 6 + 1 8 1 2 4 1 3 5 2 4 6 3 - 1 3 4 3 0 0
9 impossible
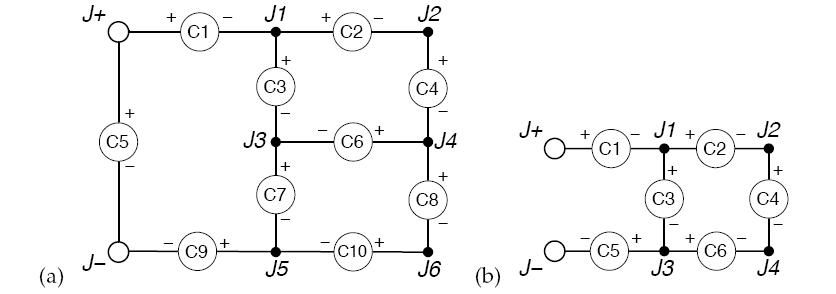
题意:有两个正负极n个节点和m个元件,每个元件告诉端点是接在哪个节点上的,并且每个元件有工作的最小电流限制,问使所有元件工作的满足条件的最小电流是多少。
思路:题目中已经有了源点S和汇点T,再添加附加源点SS和汇点TT,原图中的边的容量为INF(因为没有上限),若in[i]>0则SS向i连边容量为in[i],若in[i]<0则i向TT连边容量为-in[i],跑一次最大流,然后T向S连容量为INF的边,再跑一次最大流,判断SS的出边是否满流,若不满流则无解,否则有解输出边(T,S)的流量。
另外这类题看这里详解:点击打开链接
代码:
#include <iostream>
#include <functional>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <string>
#include <map>
#include <stack>
#include <vector>
#include <set>
#include <queue>
#pragma comment (linker,"/STACK:102400000,102400000")
#define pi acos(-1.0)
#define eps 1e-6
#define lson rt<<1,l,mid
#define rson rt<<1|1,mid+1,r
#define FRE(i,a,b) for(i = a; i <= b; i++)
#define FREE(i,a,b) for(i = a; i >= b; i--)
#define FRL(i,a,b) for(i = a; i < b; i++)
#define FRLL(i,a,b) for(i = a; i > b; i--)
#define mem(t, v) memset ((t) , v, sizeof(t))
#define sf(n) scanf("%d", &n)
#define sff(a,b) scanf("%d %d", &a, &b)
#define sfff(a,b,c) scanf("%d %d %d", &a, &b, &c)
#define pf printf
#define DBG pf("Hi\n")
typedef long long ll;
using namespace std;
#define INF 0x3f3f3f3f
#define mod 1000000009
const int maxn = 1005;
const int MAXN = 2005;
const int MAXM = 200010;
struct Edge
{
int to,next,cap,flow;
}edge[MAXM];
int tol;
int head[MAXN];
int gap[MAXN],dep[MAXN],pre[MAXN],cur[MAXN];
int n,m;
char s1[10],s2[10];
int in[MAXN];
int S,T,SS,TT;
void init()
{
tol=0;
memset(head,-1,sizeof(head));
memset(in,0,sizeof(in));
}
//加边,单向图三个参数,双向图四个参数
void addedge(int u,int v,int w,int rw=0)
{
edge[tol].to=v; edge[tol].cap=w; edge[tol].next=head[u];
edge[tol].flow=0; head[u]=tol++;
edge[tol].to=u; edge[tol].cap=rw; edge[tol].next=head[v];
edge[tol].flow=0; head[v]=tol++;
}
//输入参数:起点,终点,点的总数
//点的编号没有影响,只要输入点的总数
int sap(int start,int end,int N)
{
memset(gap,0,sizeof(gap));
memset(dep,0,sizeof(dep));
memcpy(cur,head,sizeof(head));
int u=start;
pre[u]=-1;
gap[0]=N;
int ans=0;
while (dep[start]<N)
{
if (u==end)
{
int Min=INF;
for (int i=pre[u];i!=-1;i=pre[edge[i^1].to])
if (Min>edge[i].cap-edge[i].flow)
Min=edge[i].cap-edge[i].flow;
for (int i=pre[u];i!=-1;i=pre[edge[i^1].to])
{
edge[i].flow+=Min;
edge[i^1].flow-=Min;
}
u=start;
ans+=Min;
continue;
}
bool flag=false;
int v;
for (int i=cur[u];i!=-1;i=edge[i].next)
{
v=edge[i].to;
if (edge[i].cap-edge[i].flow && dep[v]+1==dep[u])
{
flag=true;
cur[u]=pre[v]=i;
break;
}
}
if (flag)
{
u=v;
continue;
}
int Min=N;
for (int i=head[u];i!=-1;i=edge[i].next)
if (edge[i].cap-edge[i].flow && dep[edge[i].to]<Min)
{
Min=dep[edge[i].to];
cur[u]=i;
}
gap[dep[u]]--;
if (!gap[dep[u]]) return ans;
dep[u]=Min+1;
gap[dep[u]]++;
if (u!=start) u=edge[pre[u]^1].to;
}
return ans;
}
void solve()
{
for (int i=0;i<=n+1;i++)
{
if (in[i]>0) addedge(SS,i,in[i]);
if (in[i]<0) addedge(i,TT,-in[i]);
}
sap(SS,TT,n+4);
addedge(T,S,INF);
sap(SS,TT,n+4);
for (int i=head[SS];~i;i=edge[i].next)
if (edge[i].cap-edge[i].flow>0)
{
printf("impossible\n");
return ;
}
printf("%d\n",edge[head[T]].flow);
}
int main()
{
#ifndef ONLINE_JUDGE
freopen("C:/Users/lyf/Desktop/IN.txt","r",stdin);
#endif
int i,j,u,v,w;
while (scanf("%d%d",&n,&m)&&(n+m))
{
init();
S=0,T=n+1,SS=n+2,TT=n+3;
for (i=0;i<m;i++)
{
scanf("%s%s%d",s1,s2,&w);
if (s1[0]=='+') u=S;
else
{
u=0;
for (j=0;j<strlen(s1);j++)
u=u*10+s1[j]-'0';
}
if (s2[0]=='-') v=T;
else
{
v=0;
for (j=0;j<strlen(s2);j++)
v=v*10+s2[j]-'0';
}
in[v]+=w;
in[u]-=w;
addedge(u,v,INF);
}
solve();
}
return 0;
}
版权声明:本文为博主原创文章,未经博主允许不得转载。
Crazy Circuits (hdu 3157 流量有上下限的最小流)
原文:http://blog.csdn.net/u014422052/article/details/48005815