网易公开课，第3，4课
notes，http://cs229.stanford.edu/notes/cs229-notes1.pdf
前面讨论了线性回归问题， 
符合高斯分布，使用最小二乘来作为损失函数
下面继续讨论分类问题，分类问题和回归问题不同在于Y的取值是离散的
我们先讨论最简单的binary
classification，即Y的取值只有0和1
对于这样的问题是否可以继续使用线性回归模型，当然是可以的，但是不是非常适合
原因如下，
首先线性模型的Y取值是没有限制的，而二元分类的取值为[0,1]
再者，对于分类问题参考下图，以0.5为分界线，大于则取1，小于则取0
那么其实只有在分界线周围的样本点对分类模型会有比较大的影响，而比较远的样本点其实对模型没啥影响
但对于线性模型而言，增加任何样本点都会对模型产生相同的影响
所以换句话说，其实对于二元分类，并不真正符合线性模型
所以提出logistic回归模型
Logistic function（Sigmoid function）
下面给出H函数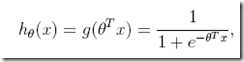 
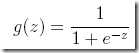
由这个函数生成的曲线称为Sigmoid曲线，这个曲线很有说道，参考http://t.cn/8st3jG1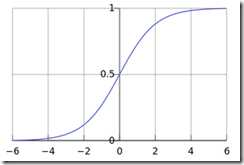
先不从数学上说为什么这个模型中二元分类上比线性模型好，单纯从图形上看就可以得到直观的结论
首先Y值域在[0,1]，其次图形中中间陡峭而两边平缓，符合二元分类的样本点特性
确定了模型，下面要做的是fit最优的θ，仍然是采用最大似然法，即找出对训练数据可能性最大的那个θ
前面对于线性回归问题，符合高斯分布，最终我们由最大似然推导出最小二乘回归
但是对于二元分类，符合伯努利分布（the Bernoulli distribution），看看由最大似然可以推导出什么
首先给出伯努利分布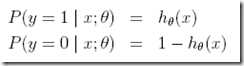 
是否好理解，给定x;θ，y=1的概率等于h的值，看看图中，当然是h的值越大越可能为1，越小越可能为0
那么这个式子可以合并写成，比较tricky的写法，Y为0或1，总有一项为1 
那么θ的似然函数定义为，θ的可能性取决于模型对训练集拟合的好坏
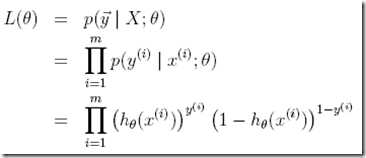
同样为了数学计算方便，定义log likelihood，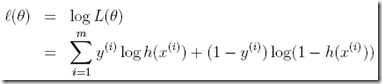 
很显然，对于伯努利分布，这里无法推导出最小二乘呵呵
下面要做的是找到θ使得?(θ)最大，由于这里是找最大值而非最小值，所以使用梯度上升（gradient ascent），道理是一样的
首先计算梯度，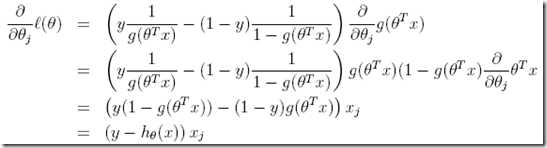 
所以最终随机梯度上升rule写成， 
这个梯度公式，奇迹般的和线性回归中的梯度公式表面上看是一样的，可以仔细比较一样的
之所以说表面上，是因为其中的
是不同的，这里是logitics函数
Andrew Ng机器学习公开课笔记 -- Logistic Regression,布布扣,bubuko.com
Andrew Ng机器学习公开课笔记 -- Logistic Regression
原文：http://www.cnblogs.com/fxjwind/p/3631281.html