POJ 2527 Polynomial Remains 多项式运算

Description

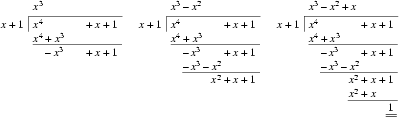Given the polynomial 
a(x) = a_n xⁿ + ... + a₁ x + a₀,
compute the remainder r(x) when a(x) is divided by x^k+1.

Input

Output

Sample Input

5 2
6 3 3 2 0 1
5 2
0 0 3 2 0 1
4 1
1 4 1 1 1
6 3
2 3 -3 4 1 0 1
1 0
5 1
0 0
7
3 5
1 2 3 4
-1 -1

Sample Output

3 2
-3 -1
-2
-1 2 -3
0
0
1 2 3 4

Source

Alberta Collegiate Programming Contest 2003.10.18

AC代码

#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
int main(){
    int n,k;
    int my[10000+10];
    while(cin>>n>>k){
        if(n==-1&&k==-1)break;
        for(int i=0;i<=n;i++)cin>>my[i];
        ///for(int i=n;i>0;--i)cout<<my[i]<<"x^"<<i<<'+';
        ///cout<<my[0]<<'\12';
        for(int i=n;i>=k;--i){
            if(my[i]==0)continue;
            my[i-k]=my[i-k]-my[i];
            my[i]=0;
        }
        int len=n;
        while(len>=0&&!my[len])len--;
        for(int i=0;i<len;++i)cout<<my[i]<<' ';
        cout<<my[len]<<'\12';
    }
    return 0;
}

POJ 2527 Polynomial Remains 多项式运算

原文：http://blog.csdn.net/zp___waj/article/details/47609147