Longest Common Subsequence Problem

The longest common subsequence (LCS) problem is the problem of finding the longest subsequence common to all sequences in a set of sequences (often just two sequences). It differs from problems of finding common substrings: unlike substrings, subsequences are not required to occupy consecutive positions within the original sequences.

https://en.wikipedia.org/wiki/Longest_common_subsequence_problem

LCS function defined[edit]

Let two sequences be defined as follows: X = (x₁, x₂...x_m) and Y = (y₁, y₂...y_n). The prefixes of X are X_{1, 2,...m}; the prefixes of Y are Y_{1, 2,...n}. Let LCS(X_i, Y_j) represent the set of longest common subsequence of prefixes X_i and Y_j. This set of sequences is given by the following.

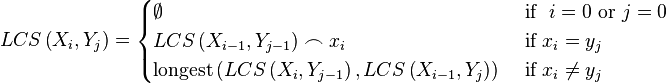
To find the longest subsequences common to X_i and Y_j, compare the elements x_i and y_j. If they are equal, then the sequence LCS(X_i-1, Y_j-1) is extended by that element, x_i. If they are not equal, then the longer of the two sequences, LCS(X_i, Y_j-1), andLCS(X_i-1, Y_j), is retained. (If they are both the same length, but not identical, then both are retained.) Notice that the subscripts are reduced by 1 in these formulas. That can result in a subscript of 0. Since the sequence elements are defined to start at 1, it was necessary to add the requirement that the LCS is empty when a subscript is zero.

Computing the length of the LCS

The function below takes as input sequences X[1..m] and Y[1..n] computes the LCS between X[1..i] and Y[1..j] for all 1 ≤ i ≤ m and 1 ≤ j ≤ n, and stores it in C[i,j]. C[m,n] will contain the length of the LCS of X and Y.

function LCSLength(X[1..m], Y[1..n])
    C = array(0..m, 0..n)
    for i := 0..m
       C[i,0] = 0
    for j := 0..n
       C[0,j] = 0
    for i := 1..m
        for j := 1..n
            if X[i] = Y[j]
                C[i,j] := C[i-1,j-1] + 1
            else
                C[i,j] := max(C[i,j-1], C[i-1,j])
    return C[m,n]

Example Question:
http://www.lintcode.com/en/problem/longest-common-subsequence/
http://www.lintcode.com/en/problem/longest-common-substring/

Longest Common Subsequence Problem

原文：http://www.cnblogs.com/midan/p/4688049.html